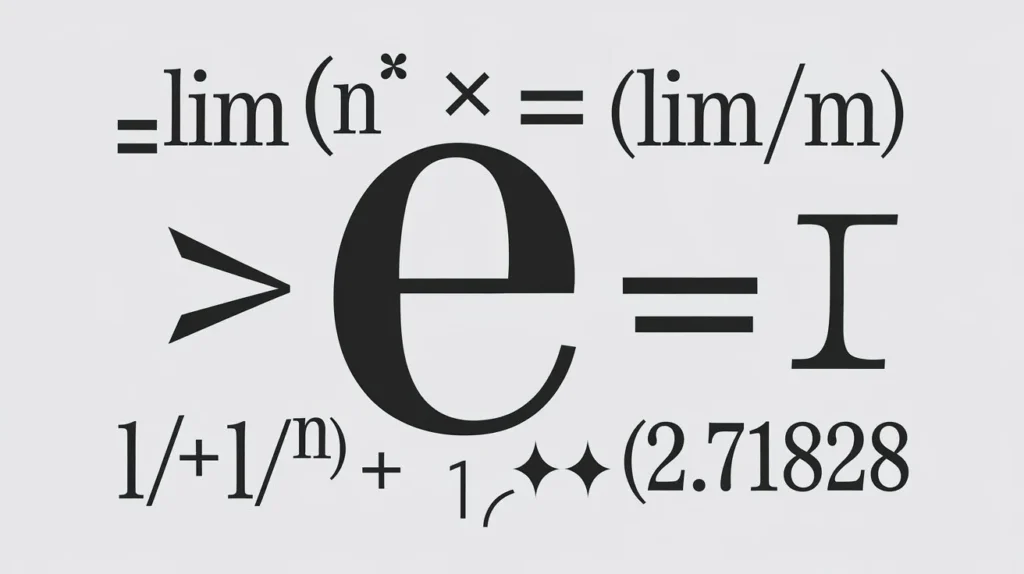What Does E Mean in Math Explained for Students and Beginners For 2026

If you have ever studied algebra, calculus, or even finance, you have probably seen the letter e appear in equations and wondered what it actually means. Unlike a variable, e is a special mathematical constant with a fixed value of approximately 2.71828. 

It may look confusing at first, but e plays a crucial role in describing growth, change, and natural processes. From population growth and compound interest to calculus and logarithms, e shows up whenever something changes continuously over time. 

Understanding what e means in math can make many complex formulas feel more logical and easier to understand. 

In this article, you’ll learn what e is, where it comes from, why it is so important in mathematics, and how it is used in real-world applications. 

By the end, you’ll have a clear, intuitive understanding of why e is one of the most important numbers in math.

What Is e in Math? (Simple Explanation)

In mathematics, e is a special constant, just like π (pi). It is not a variable and not something that changes from problem to problem. The value of e is approximately 2.71828, and its decimal goes on forever without repeating. Because of this, e is classified as an irrational number. When people ask, “what does e mean in math?”, the simplest answer is that e is the natural base used to describe continuous growth and change.

Unlike numbers we choose for convenience, e appears naturally in mathematics. It shows up when we study how things grow smoothly over time rather than in steps. For example, when money earns interest continuously, when a population grows without interruption, or when a substance decays gradually, e is the number that best models those processes.

One important thing to understand is that e is a fixed constant, not just the letter “e” standing for something else. Just as π always represents the ratio of a circle’s circumference to its diameter, e always represents the same numerical value and idea. Mathematicians use e because it has unique properties that make calculations easier, especially in calculus.

In short, e is the number that describes how quantities change when growth is continuous and natural. Once you understand this idea, many formulas involving e start to make much more sense, instead of feeling random or confusing.

Why Is e Called Euler’s Number?

The number e is often called Euler’s number because of the mathematician Leonhard Euler, one of the most influential figures in the history of mathematics. Although Euler did not originally discover the number e, he was the person who studied it deeply, gave it its modern notation, and showed just how important it is across many areas of math.

The idea behind e first appeared in the early study of compound interest during the 17th century. Mathematicians noticed that when interest is compounded more and more frequently, the final amount approaches a fixed number. This mysterious limit is what we now call e. Later, Euler explored this number extensively and recognized that it plays a central role in exponential functions, logarithms, and calculus.

Euler was the first to consistently use the letter e to represent this constant, and his work connected e to many powerful mathematical ideas. He showed how e relates to exponential growth, complex numbers, and trigonometry, most famously through Euler’s formula, which links e, π, and imaginary numbers in a single elegant equation.

Because of Euler’s massive contributions and clear explanations, the number became permanently associated with his name. Today, calling e “Euler’s number” is a way of honoring his work and acknowledging how essential e is to modern mathematics. Thanks to Euler, e is no longer just a strange constant, but a foundational concept used throughout science and engineering.

Where Does the Number e Come From?

The number e comes from studying what happens when growth becomes continuous rather than happening in steps. One of the easiest ways to understand its origin is through the idea of compound interest. Imagine you invest money and earn interest once per year. If the interest is compounded more frequently—monthly, daily, or even every moment—you might expect the final amount to keep increasing. However, mathematicians discovered that this growth approaches a fixed limit. That limit is the number e.

As the number of compounding periods increases without bound, the resulting expression settles closer and closer to 2.71828. This behavior is described using limits, a fundamental concept in calculus. In simple terms, a limit shows what value a quantity approaches as something continues indefinitely. When growth is compounded infinitely many times at an infinitely small rate, the limit of that process produces e.

What makes e special is that it appears naturally, without being forced or chosen. It is not based on human-made measurements like inches or degrees. Instead, it emerges from the mathematics of growth itself. That is why e is called the natural base for exponential functions.

This origin explains why e appears so often in problems involving change over time, such as population growth, radioactive decay, and cooling processes. Whenever something grows or shrinks smoothly and continuously, the math behind it tends to lead back to e, making it one of the most natural and important numbers in mathematics.

Understanding e Through Growth and Change

One of the best ways to understand what e means in math is to think of it as the number that describes continuous growth and change. In real life, many processes do not grow in neat, separate steps. Instead, they change smoothly at every moment. This is where e becomes essential. It provides the most accurate mathematical way to model these natural processes.

To see the difference, consider discrete growth versus continuous growth. Discrete growth happens in steps, such as getting paid once a month. Continuous growth, on the other hand, is like bacteria multiplying, heat spreading, or money earning interest every instant. When growth is continuous, formulas based on e describe the behavior far better than formulas using other numbers.

Mathematically, e has a unique property: when something grows at a rate proportional to its current size, e naturally appears in the solution. This means the more there is of something, the faster it grows, and that pattern leads directly to exponential functions with base e. This is why e is often called the “natural growth constant.”

Nature itself seems to favor e. From population models to chemical reactions, equations involving e show up repeatedly because they match how the real world behaves. This is not a coincidence—it is a result of how continuous change works.

Understanding e through growth helps remove the mystery around it. Instead of seeing e as a strange number, you can think of it as the mathematical language used to describe smooth, uninterrupted change over time.

What Is e Used for in Math?

The number e is used throughout mathematics because it simplifies the way we describe change, growth, and decay. One of its most important uses is in exponential functions, especially expressions like eˣ. These functions are ideal for modeling situations where the rate of change depends on the current value, which is common in both math and science.

Another major use of e is in calculus. The function eˣ is unique because its derivative is itself. In simple terms, this means the rate at which eˣ changes is exactly equal to its current value. No other number has this property, which makes e incredibly useful for solving problems involving rates of change. Because of this, equations using e are often easier to differentiate and integrate than those using other bases.

e is also the foundation of natural logarithms, written as ln. The natural logarithm is the inverse of the exponential function with base e, and it appears frequently in calculus, algebra, and applied mathematics. Natural logs are especially useful for solving exponential equations and analyzing growth patterns.

Beyond pure math, e is essential in probability, statistics, and differential equations. It appears in formulas that describe normal distributions, decay processes, and dynamic systems. In short, e is used whenever mathematics needs to describe how something changes continuously, making it one of the most powerful and widely used constants in the entire field.

E in Calculus (Beginner to Intermediate)

In calculus, the number e plays a central role because it perfectly connects functions with their rates of change. One of the most important facts students learn is that the derivative of eˣ is eˣ itself. This means that as the value of the function changes, its rate of change matches it exactly at every point. No other base has this property, which is why e is considered the most “natural” base for exponential functions.

To understand why this matters, remember that calculus is largely about studying how things change. When an exponential function uses e as its base, calculations become simpler and more elegant. Derivatives and integrals involving e often follow straightforward rules, while other bases require extra constants and adjustments. This makes e the preferred choice for mathematicians and scientists.

e is also essential in solving differential equations, which are equations that relate a function to its derivatives. Many real-world systems—such as population growth, radioactive decay, and cooling processes—are described using differential equations. The solutions to these equations almost always involve e, because continuous change naturally leads to exponential behavior.

Another important idea is the connection between e and limits. Calculus defines e using a limit that describes growth happening in infinitely small steps. This definition helps explain why e appears so often when working with derivatives and integrals.

Overall, e acts as a bridge between functions and their behavior over time. Once you understand its role in calculus, many formulas that once seemed complicated start to feel logical and well-connected.

What Is the Natural Logarithm (ln)?

The natural logarithm, written as ln, is closely connected to the number e. In simple terms, ln is the inverse of the exponential function with base e. This means that if e raised to a certain power gives a number, the natural logarithm tells you what that power is. Because of this relationship, ln and e often appear together in mathematical formulas.

Natural logarithms are used because they make working with exponential growth and decay much easier. When a problem involves continuous change, using ln helps simplify equations and reveals clear relationships between variables. In calculus, natural logarithms are especially useful because their derivatives and integrals follow clean, predictable rules.

It is important to understand the difference between ln and log. While ln always means a logarithm with base e, log may refer to a logarithm with base 10 or another base, depending on the context. In higher-level math and science, ln is often preferred because it naturally aligns with exponential functions involving e.

Natural logarithms are commonly used to solve equations where a variable appears in an exponent. They also appear in formulas for compound interest, population growth, and radioactive decay. Because e models continuous change so accurately, ln becomes the most natural way to “undo” that change mathematically.

Understanding ln helps deepen your understanding of e itself. Once you see how exponential functions and natural logarithms work together, many complex-looking formulas become easier to interpret and apply.

e vs π: What’s the Difference?

Both e and π (pi) are famous mathematical constants, but they represent very different ideas. While π is mainly connected to geometry, e is closely tied to growth and change. Understanding the difference between them helps clarify when and why each one is used.

The number π comes from circles. It represents the ratio of a circle’s circumference to its diameter, which is why it appears in formulas involving circles, spheres, and waves. Whenever a problem involves angles, rotations, or circular motion, π is usually involved. Its meaning is geometric and spatial.

On the other hand, e comes from studying continuous growth. It appears in problems where quantities increase or decrease smoothly over time. This includes population growth, compound interest, decay processes, and calculus. Instead of describing shapes, e describes how things change.

Another key difference is how they are used in formulas. π often appears in trigonometry and geometry, while e dominates calculus, exponential functions, and logarithms. Both numbers are irrational and have infinite, non-repeating decimals, but their roles in mathematics are very different.

Despite their differences, e and π sometimes come together in advanced mathematics, most famously in Euler’s formula. This connection shows that geometry and growth are deeply linked at a higher level.

In short, π is the constant of circles, while e is the constant of natural growth. Knowing which one applies depends on whether your problem involves shape and rotation or continuous change over time.

Real-World Applications of e

The number e is not just a theoretical concept—it plays a major role in many real-world applications. One of the most common examples is finance, particularly in formulas for compound interest. When interest is compounded continuously, e is used to calculate how money grows over time. This helps banks, investors, and economists model realistic financial growth.

In biology, e is used to model population growth. When a population grows at a rate proportional to its current size, exponential equations involving e describe the process accurately. Similar models are used to study the spread of bacteria, viruses, and even information through social networks.

e also appears in physics and chemistry, especially in decay processes. Radioactive decay, chemical reactions, and cooling laws often rely on exponential functions with base e. These equations help scientists predict how systems change continuously over time.

In statistics and probability, e plays a key role in probability distributions, such as the normal distribution. It is also used in data science and machine learning, where exponential functions help model probabilities and optimize algorithms.

Engineering, medicine, and environmental science all rely on formulas involving e to describe real-life systems. Whether it is modeling drug absorption in the body or predicting temperature changes, e provides a reliable mathematical tool.

These real-world uses show why e is so important. It is not just a number learned in school, but a constant that helps explain and predict how the world changes naturally.

How to Recognize When to Use e

One common question students ask is how to know when to use e instead of another number. The key idea to remember is that e is used whenever a problem involves continuous change. If something is growing or shrinking smoothly at every moment, there is a strong chance that e belongs in the formula.

A major clue is the phrase “rate proportional to its current value.” This wording appears often in math, physics, and biology problems. When the rate of change depends on how much of something already exists, the solution usually involves an exponential function with base e. Population growth, radioactive decay, and continuously compounded interest all follow this pattern.

Another sign is the use of calculus, especially derivatives and integrals. If a problem asks about rates of change, differential equations, or natural logarithms, e is almost always involved. The natural logarithm ln specifically tells you that the base is e, not 10 or any other number.

You will also see e in formulas designed to model real-world behavior accurately. Scientists and engineers prefer e because it matches how natural systems behave over time. This makes equations easier to work with and more realistic.

In contrast, if a problem involves geometry, circles, or angles, π is more likely the correct constant. If growth happens in clear steps, another base might be used instead of e.

By focusing on whether change is continuous and natural, you can quickly recognize when e is the right choice and apply it with confidence.

next and 250 words count

Is e an Irrational or Transcendental Number?

The number e is both irrational and transcendental, which makes it especially interesting in mathematics. Understanding these terms helps explain why e behaves differently from ordinary numbers.

An irrational number is a number that cannot be written as a simple fraction of two integers. Its decimal expansion goes on forever without repeating. The number e fits this definition because its digits continue infinitely and never follow a repeating pattern. No fraction, no matter how precise, can represent e exactly. This is why we often use approximations like 2.71828 when working with it.

Beyond being irrational, e is also transcendental. A transcendental number is not the solution to any algebraic equation with whole-number coefficients. In simpler terms, e cannot be “solved for” using standard polynomial equations. This property makes e even more complex than numbers like √2, which are irrational but not transcendental.

The fact that e is transcendental was proven in the 19th century and was a major achievement in mathematics. It confirmed that e is fundamentally different from most numbers students encounter in algebra.

These properties explain why e appears so naturally in advanced mathematics. Its infinite, non-repeating structure aligns perfectly with continuous processes and change. Knowing that e is both irrational and transcendental highlights why it cannot be simplified or replaced—and why it remains one of the most important constants in math.

Common Misconceptions About e

Because e appears in many advanced formulas, it is often misunderstood by students and beginners. One common misconception is that e is just a variable, similar to x or y. In reality, e is a fixed constant with a specific value, just like π. It never changes from one equation to another.

Another misunderstanding is thinking that e equals 2.7 exactly. While 2.71828 is a common approximation, the true value of e has infinitely many digits that never repeat. Any decimal representation you see is only an estimate, not the exact number.

Some people also believe that e can be replaced with any other base in exponential equations without changing much. This is not true. Using e simplifies calculus because the derivative and integral of eˣ have unique properties that do not work the same way with other bases.

There is also a misconception that e is only used in calculus. While it is extremely important in calculus, e also appears in finance, biology, physics, statistics, and computer science. Its usefulness goes far beyond classroom math.

Finally, some think e is an invented or arbitrary number. In fact, e arises naturally from studying growth and limits. Mathematicians did not choose it randomly—it emerged because it best describes continuous change.

Clearing up these misconceptions helps make e feel less intimidating. Once you see it as a natural and essential constant, its frequent appearance in math starts to make sense.

Simple Examples of e in Action

Seeing e in practical examples can make its meaning much clearer. One simple example comes from exponential growth. Suppose a quantity grows at a rate proportional to its current size. The mathematical model for this situation uses the function eˣ, because it perfectly represents continuous growth. As time increases, the value grows smoothly without sudden jumps, which matches many real-life processes.

Another easy example is continuous compound interest. If you invest money and interest is added continuously rather than yearly or monthly, the formula involves e. This shows how even small, constant growth over time can lead to larger results than step-based growth. Financial institutions use this model to better understand long-term growth trends.

In calculus, e appears in simple differentiation problems. When you take the derivative of eˣ, the result is eˣ again. This makes it much easier to analyze how fast a quantity is changing at any moment. Because of this property, many real-world systems are modeled using functions based on e.

e also appears in decay examples. For instance, radioactive substances lose mass continuously over time. Equations using e accurately describe how quickly the substance decays and how much remains after a certain period.

These examples show that e is not abstract or random. It appears whenever math is used to describe smooth, continuous change. By working through simple cases like growth, interest, and decay, you can see how e naturally fits into real-world problems and why it is such a powerful mathematical constant.

Frequently Asked Questions 

What does e stand for in math?
The letter e does not stand for a word. It is simply the symbol chosen to represent a specific mathematical constant, now known as Euler’s number, with a value of approximately 2.71828.

Why is e equal to 2.71828?
The value of e comes from a mathematical limit related to continuous growth. When growth is compounded more and more frequently, the resulting value approaches 2.71828, which is why this number defines e.

Is e more important than π?
Neither number is more important than the other—they serve different purposes. π is essential for geometry and circles, while e is crucial for growth, change, and calculus.

Who discovered e?
The concept of e emerged from early studies of compound interest. Leonhard Euler later studied it extensively, named it, and showed its importance, which is why it is associated with his name.

Can e be calculated exactly?
No, e cannot be written exactly as a fraction or a finite decimal. It has infinitely many non-repeating digits, so we can only use approximations.

Why does e appear so often in math?
e appears frequently because it naturally describes continuous change. Whenever a system grows or decays smoothly over time, the mathematics behind it often leads to e.

These common questions summarize why e is such a central and fascinating number in mathematics.

Summary: 

The number e may seem confusing at first, but it is one of the most important and natural constants in mathematics. Rather than being an arbitrary value, e emerges naturally when we study continuous growth and change. Its approximate value of 2.71828 appears whenever something grows or decays smoothly over time, making it essential for understanding real-world processes.

Throughout mathematics, e plays a central role in exponential functions, natural logarithms, and calculus. Its unique property—where the derivative of eˣ is eˣ itself—makes it especially powerful for studying rates of change. Because of this, mathematicians, scientists, and engineers rely on e to model everything from population growth and compound interest to radioactive decay and probability distributions.

Unlike constants tied to geometry, such as π, e is connected to behavior and change. It helps explain how systems evolve rather than how shapes are measured. This distinction explains why e appears so frequently in advanced math and applied sciences.

Understanding what e means in math helps demystify many formulas that students often find intimidating. Once you recognize e as the natural number of continuous growth, its repeated appearance starts to feel logical rather than random.

In short, e matters because it provides a clear, elegant way to describe how the world changes. Learning its meaning is a key step toward mastering higher-level mathematics and understanding the patterns behind natural phenomena.