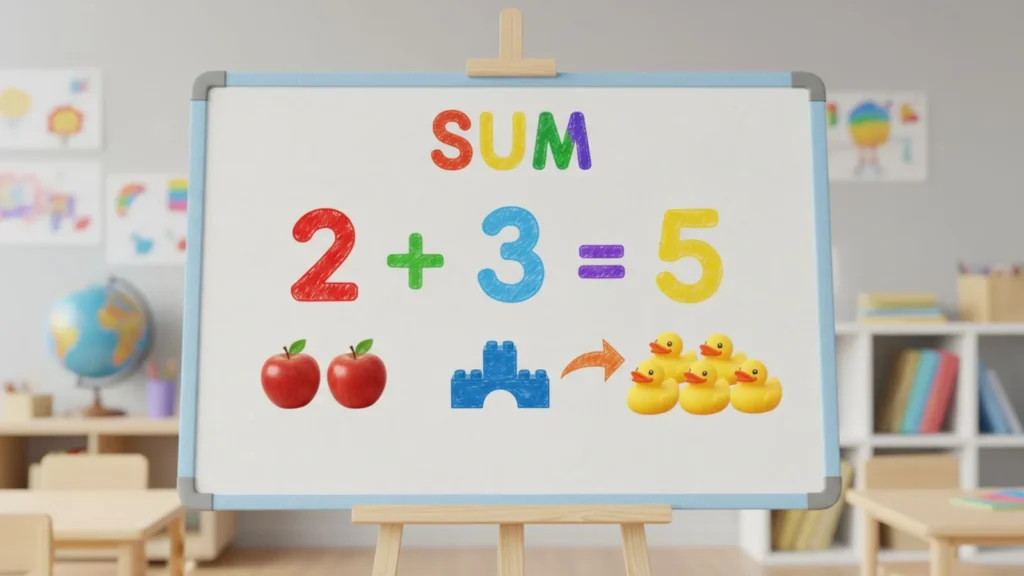In mathematics, the term “sum” is one of the most fundamental concepts you will encounter. Simply put, a sum is the result of adding two or more numbers together.
From the moment we start learning basic arithmetic, understanding sums is essential because it forms the foundation for almost all other areas of math, including subtraction, multiplication, algebra, and even statistics.
Sums are not just abstract numbers on a page they appear in our everyday lives constantly.
You are calculating the total cost of groceries, adding up scores in a game, or figuring out how much time has passed, sums help us make sense of quantities and numbers around us.
In this article, we will explore the meaning of sum, see multiple examples, learn how to calculate it, and discover its importance in both mathematics and real-world applications.
Definition of Sum
In mathematics, a sum is the result you get when you add two or more numbers together. It is one of the basic building blocks of arithmetic and is essential for understanding more advanced math topics. When you see the addition symbol “+”, it means you are combining numbers to find their sum. For example, in the expression 4 + 7, the sum is 11.
The concept of sum is not limited to just numbers; it can also apply to variables, decimals, fractions, and even angles in geometry. In algebra, the sum of variables like x + y represents a combined value of unknown quantities. Similarly, in statistics, sums are used to calculate averages, totals, and other important measures.
It is important to understand the difference between sum, total, and addition. While addition is the process of combining numbers, the sum is the final result of that process. Understanding sums helps build a strong foundation for learning other operations like subtraction, multiplication, and division. With practice, calculating sums becomes quicker and easier, and it is a skill you will use frequently in daily life.
Understanding Sum Through Addition
To truly understand what a sum is, it helps to connect it with the concept of addition. Addition is the mathematical operation of combining two or more numbers, and the sum is the result of that combination. For example, if you add 3 + 5, the sum is 8. This simple idea is the foundation of arithmetic and is used everywhere in math.
There are a few important properties of addition that make working with sums easier:
- Commutative Property – The order of numbers does not change the sum. For example, 4 + 7 = 7 + 4 = 11.
- Associative Property – When adding three or more numbers, the way they are grouped does not change the sum. For instance, (2 + 3) + 5 = 2 + (3 + 5) = 10.
- Identity Property – Adding zero to any number does not change the sum. For example, 9 + 0 = 9.
By understanding these properties, calculating sums becomes faster and more flexible. Sums are not just about memorizing numbers—they are about recognizing patterns and relationships between numbers, which is why they are so important in both simple arithmetic and advanced mathematics.
Examples of Sum
Understanding sums becomes much easier when we look at examples. Let’s start with simple numbers. If you add 3 + 5, the sum is 8. Similarly, adding multiple numbers like 2 + 4 + 6 gives a sum of 12. These basic examples show how sums are calculated in everyday arithmetic.
Sums are not limited to positive numbers. For instance, adding a negative number works the same way: 7 + (–3) = 4. You can also find the sum of decimals, such as 2.5 + 3.7 = 6.2, or fractions, for example, 1/2 + 1/4 = 3/4.
Sums are also commonly used in word problems. For example: “Sara has 5 apples, and she buys 7 more. How many apples does she have now?” Here, 5 + 7 = 12, so the sum is 12 apples.
Visual examples can help beginners, such as drawing objects like coins, blocks, or apples and counting the total. By practicing with different types of numbers—whole numbers, decimals, fractions, and negatives—you can strengthen your understanding of sums and become more confident in applying addition in both math problems and real-life situations.
Sum in Different Mathematical Contexts
The concept of a sum is not limited to simple addition of numbers—it appears in many areas of mathematics, each with its own context. In algebra, for example, the sum can involve variables and constants. An expression like x + y + 5 represents the sum of unknown values and a constant, which is often simplified or solved in equations.
In geometry, sums are used to calculate angles. For instance, the sum of angles in a triangle is always 180 degrees, and the sum of angles in a quadrilateral is 360 degrees. These sums help in solving shape-related problems and designing structures accurately.
In statistics, sums are essential for analyzing data. The sum of all data points is used to calculate the mean (average), which provides insight into trends and patterns.
Sums also appear in series and sequences. For example, in an arithmetic sequence like 2, 4, 6, 8, the sum of the first n terms can be calculated using a formula. Similarly, in finance or science, sums of large sets of numbers help in calculations like total revenue, energy consumption, or measurement analysis.
Understanding how sums work in these various contexts highlights their versatility and importance in both academic and real-world applications.
Practical Applications of Sum
Sums are not just a math concept—they are used constantly in everyday life. One of the most common applications is in financial calculations. For example, when shopping, you add the prices of items to find the total cost. Similarly, when splitting a bill among friends, you calculate the sum to determine each person’s share.
In education, sums are essential for students to learn more advanced math concepts. Mastering addition and sums helps in solving algebraic equations, understanding geometry, and even tackling statistics. Teachers often emphasize sums early on because they form the foundation for more complex problem-solving skills.
Sums are also important in technology and programming. Computers frequently calculate sums to process data, analyze numbers, and generate results. For instance, spreadsheets use sums to quickly calculate totals, averages, and financial reports.
Even in daily problem-solving, sums help us plan, budget, and organize. Whether calculating the total hours worked in a week, combining distances traveled, or adding points in a game, sums make numerical reasoning simple and efficient.
Understanding sums equips us with a practical tool to handle numbers confidently, both in school and in real-life situations.
Common Misconceptions About Sum
Even though sums are one of the most basic concepts in math, many people have misconceptions about them. One common misunderstanding is confusing the sum with the product or difference. For example, some beginners might mistakenly think that 4 + 3 is 12, confusing addition with multiplication. It’s important to remember that the sum is always the result of addition.
Another misconception is that sums only involve positive numbers. In reality, sums can include negative numbers, decimals, and fractions. For instance, 7 + (–3) = 4, and 2.5 + 3.5 = 6. People sometimes forget that negative numbers and fractions also have sums that follow the same rules of addition.
Some also assume that addition order matters, but the commutative property proves otherwise: 5 + 2 = 2 + 5. Others struggle with sums of decimals or fractions due to differences in place value or denominators, thinking the process is more complicated than it actually is.
By understanding these misconceptions, learners can approach sums with clarity and confidence, making arithmetic and more advanced math concepts easier to grasp. Correct practice helps prevent mistakes and builds a stronger foundation for future learning.
Tips to Easily Calculate Sums
Calculating sums can be simple and quick if you use the right strategies and tips. One of the easiest methods is mental math. For example, you can round numbers to the nearest ten, add them, and then adjust the total. For instance, to add 48 + 37, round 48 to 50 and 37 to 40, giving 90, then subtract the 5 added extra (2 from 48 and 3 from 37) to get 85.
Using a number line is another helpful technique, especially for beginners or visual learners. You start at the first number and move forward by the value of the second number to find the sum. This method works well for both positive and negative numbers.
Grouping numbers can also make sums easier. For example, in adding 2 + 5 + 8, you can first combine 2 + 8 = 10, then add 5 to get 15. This technique, known as associative grouping, is particularly useful when working with multiple numbers.
Lastly, for larger sums, using calculators or spreadsheet software can save time and reduce errors. By practicing these strategies, calculating sums becomes faster, more accurate, and less stressful, whether you’re doing simple arithmetic or solving complex problems.
Fun Facts / Interesting Notes About Sum
While sums may seem like a basic math concept, they have interesting facts and applications that make them more fascinating than they appear. For example, addition and sums have been used for thousands of years, dating back to ancient civilizations such as the Babylonians and Egyptians, who relied on sums for trade, construction, and astronomy.
Did you know that sums are essential in computer science? Computers perform millions of addition operations every second to process data, run programs, and even display graphics. In programming, the sum of numbers in arrays or lists is a common operation used in countless applications.
Sums also play a role in puzzles and games. Popular number games like Sudoku or even scoring in board games rely on calculating sums to achieve the correct results.
Another fun fact is that sums are the foundation for large-scale calculations in science and finance. From adding distances in space exploration to calculating national budgets, sums help organize and understand huge amounts of data efficiently.
These facts show that sums are not just for classrooms—they are everywhere in the real world, making them both practical and fascinating to study.
Conclusion
In mathematics, the concept of a sum is simple yet incredibly important. At its core, a sum is the result of adding two or more numbers together, whether they are whole numbers, decimals, fractions, or even negative values. Understanding sums is not just about performing calculations—it forms the foundation for almost every other area of math, including algebra, geometry, statistics, and advanced problem-solving.
Sums are also highly practical in everyday life. From calculating the total cost of shopping, tracking time, or dividing expenses with friends, to analyzing data in science, technology, and finance, sums help us make sense of numbers and manage quantities effectively. They appear in word problems, equations, series, and even computer programming, proving their versatility and importance.
By practicing addition, understanding properties like commutative and associative rules, and learning tips for quicker calculations, anyone can become confident in finding sums. Recognizing sums in various contexts—from classrooms to real-world scenarios—demonstrates how essential this concept is in both learning mathematics and solving daily problems.
Ultimately, mastering sums is a key step toward mathematical fluency, making it easier to tackle more complex topics and develop strong numerical skills that last a lifetime.